DH算法圖解+數學證明 淺顯易懂

前幾天和同事討論IKE密鑰交換流程時，提到了Diffie-Hellman交換。DH算法最主要的作用便是在不安全的網絡上成功公共密鑰(并未傳輸真實密鑰)。但由于對于DH算法的數學原理則不清楚，因此私下對DH算法進行一個簡單學習。

1. DH算法的交互流程：

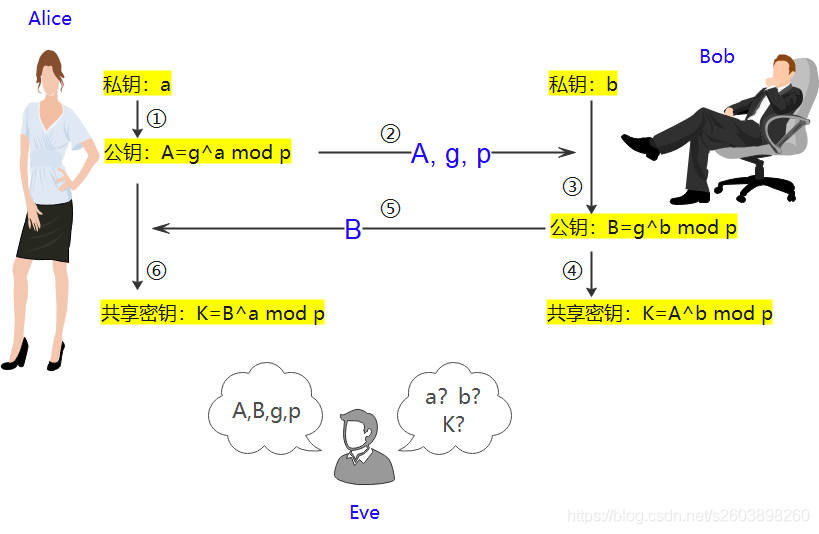
Alice和Bob都有一個只有自己知道的私鑰，在特定規則(g， a， p)下生成自己的公鑰A; Alice將自己的公鑰A，連同g， p共同發給BobBob在收到Alice發送來的公鑰A， g， p后，先使用相同的規則((g， a， p))生成自己的公鑰B;在使用Alice的公鑰A計算生成共享密鑰KBob將自己的公鑰B發送給Alice即可。(Alice已經有g， p， 因此無需在發送)Alice在接收到Bob的公鑰B后，使用相同的規則計算成功共享密鑰K

至此，Alice 和 Bob便同時擁有了共享密鑰K。此時由于各自的私鑰a，b未在互聯網上傳播，因此即使存在窺探者Eve，他僅通過公開的A\B\g\p在短時間內無法破解出a，b，K。因此DH算法便可以在不安全的網絡上協商出密鑰，基于此構建安全的加密通道。

2. 疑問：Alice和Bob最后計算的K值一樣嗎？

對于DH整個交互流程來說，比較簡單，基本都可以理解。但是忽然說最后的K值相等，這多少有點突然和難以置信，讓人有點猝不及防。

書本上都是這樣解釋的：

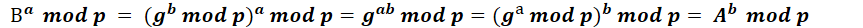
所以Alice和Bob的共享密鑰K是相同的。但是，總感覺沒有get到要領和精髓。因為我不知道mod（求余）的運算規則，不知道如下等式是否成立？？？

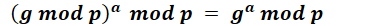
因此半夜凌晨1點從剛暖熱乎的被窩又爬了出來，想要證明下他們給的公式是否正確( 其實當成定理記住也就OK了，不過我嘛，還是爬起來了)。證明這個公式也很簡單：將求余運算轉換為加減乘除運算，然后利用二項式展開公式便可以得到答案。

至于為什么要將求余運算轉換為加減乘除四則運算，原因是我不知道求余算法的規則，不然我也不需要多此一舉了。

證明開始：

令：

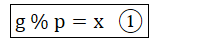
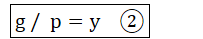
則：

根據①②式可得：

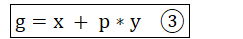
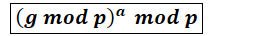
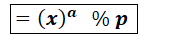
將③帶入上式可得：

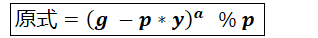
使用二項式展開公式將