ECDH算法介紹
1.1、橢圓曲線介紹
ECC(Elliptic Curves Cryptography,橢圓曲線加密)是一種公開密鑰算法。1985年,Neal Koblitz和Victor Miller分別獨立提出了ECC。基本形狀可以參考如下圖:

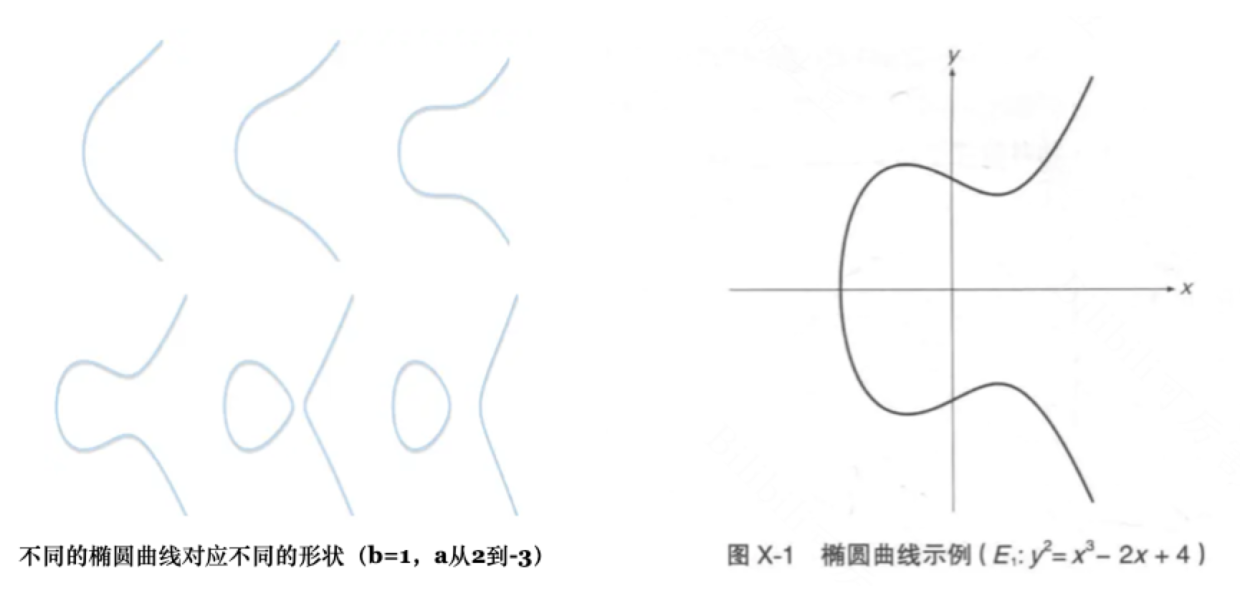
圖3:橢圓曲線示例
1.2、圖解橢圓曲線
橢圓曲線有兩個特點:
如果你在上方隨便畫一個點,那么下方也一定有一個對稱的點,上下方距離水平線X軸是相同的。隨便在圖形上畫兩個點,讓這兩個點連成線然后延長會經過第三個點,當然除了垂直線以外。
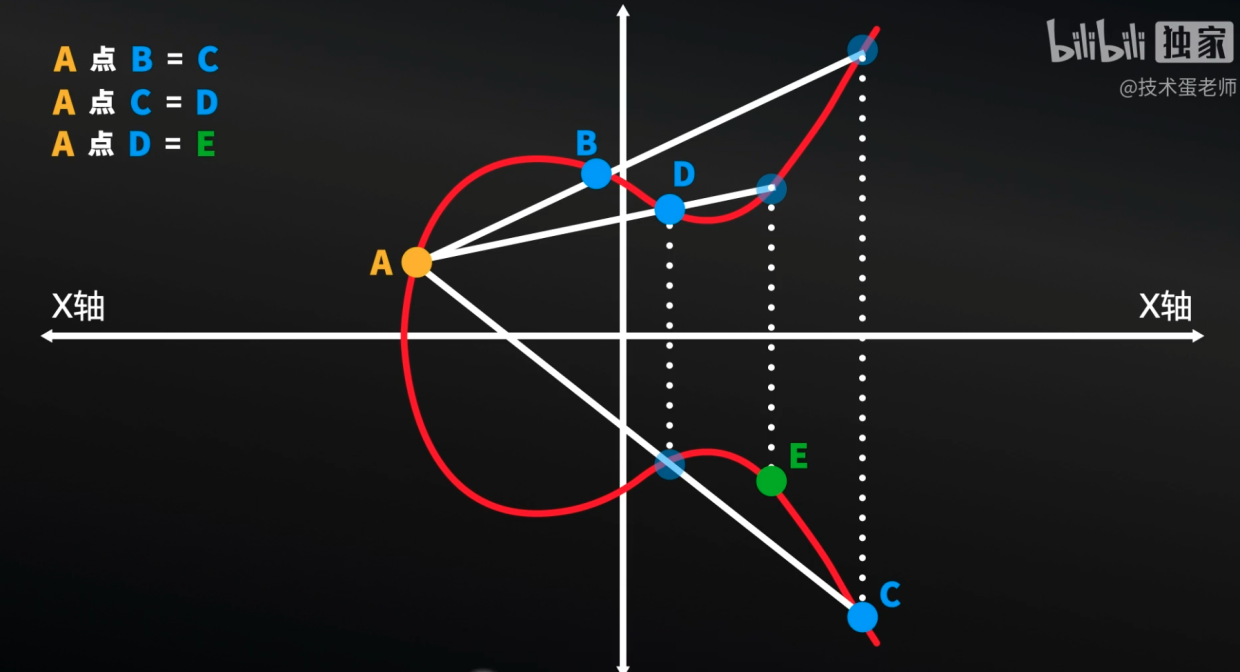
圖4:曲線A點到E點步驟
根據這兩個特點我們就可以做文章了。如果有A,B兩個點,延長以后會經過第三個點,而這第三個點以X軸為中心是會有一個點與其對稱,我們就把這個對稱的點先稱為C點。這里頭就像是運算過程,A和B得出C,在這里我就把運算過程稱為 “點運算”,A點B得到C,這個 “點運算”其實就是橢園曲線上的加法運算,但為了讓你們不與傳統加法運算弄混,這里先使用“點運算”的說法。
現在我們把A和C進行連線,同樣經過了第三個點,第三個點也有一個對稱的點,這里稱為D點,也就是A點C得到D,我們再把A和D連線,也經過了第三個點,第三個點也有一個對稱的點,這里稱為E點,也就是A點D得到E。
問題:已知起點是A,終點是E,請問起點A經過多少次點運算得到E?我們很難知道經過了多少次,這就很符合我們前面說的公鑰加密的特點:正向簡單,逆向困難
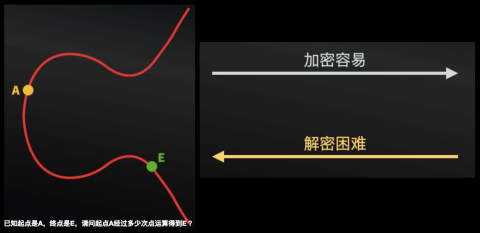
圖5:加密容易,解密困難
我們還要考慮一種特殊情況,如果我們取一個點,命名為P,然后畫一條直線,結果發現這條直線只能與橢圓曲線相交于一個點,而不是剛剛所說的一共有三個點,這種情況怎么定義運算呢?
首先解釋一下這是一條切線,如果不記得什么是切線,那就想象這里有一個圓,而切線是垂直于經過切點的半徑,還不明白也沒關系,現在點P身處的這條直線相交橢圓曲線后,也有一個對稱的點,這里先命名為Q點, 現在重點來了!因為點P初始沒有和其他點連成線,不是剛剛那種開始就有兩個點來連線,因此這里就認為是P點P的運算,也就是自己點自己,所以Q就是P點P的運算結果,也就是兩介P得到Q,我們就把點Q稱為2P,因為是兩個P得出的點,你也可以理解為P+P=2P。
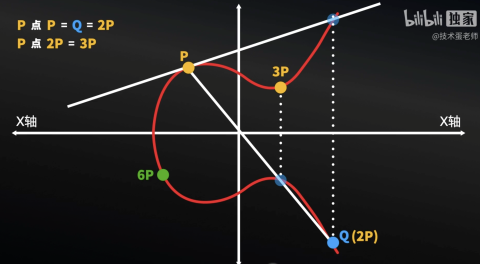
圖6:曲線中的切線
現在P與2P連線,也經過了第三個點,第三個點也有一個對稱的點,P+2P就等于3P,這個點就是3P,那么這個過程可以一直延續下去,我們是可以得到6P這個點的,6P這個點就很有靈性了,比如3P點3P,兩次的話可以得到6P,也就是3P乘以2得到6P,那2P點2P,三次的話也可以得到6P,也就是2P乘以3得到6P,其實就是簡單的乘法問題,只不過是橢園曲線上的,不要小看這簡單的表示方法,等會你可能就會對著屏幕說“握草”。

圖7:6P的生成
1.3、笛福赫爾曼(Diffie-Hellman)算法
DH 算法又稱“Diffie–Hellman 算法”,像往常的算法名字一樣,這是用倆個數學牛人的名字來命名的算法,實現安全的密鑰交換,通訊雙方在完全沒有對方任何預先信息的條件下通過不安全信道創建起一個密鑰。
如下圖示例:首先兩個要溝通的對象需要確定兩個參數,參數P和參數G,參數P,故名意思是一個質數,因為P是Prime的縮寫,而參數G是Generator的縮寫,這里就不詳細解釋G的緣由了,因為涉及到一些數學的知識。這里我選一個簡單的質數23,因為23乘以1等于23,沒有其它整數相乘可以得到23了,而參數G這里選擇5,這兩個參數是可以公開的,所以黑客知道也沒關系。
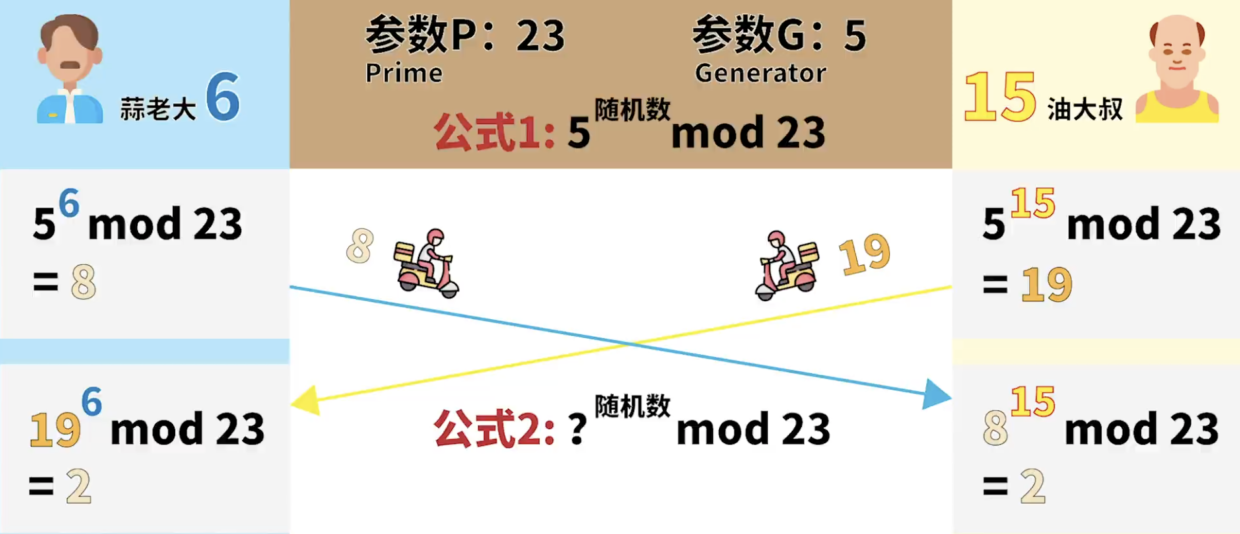
圖8:DH算法示例
現在就可以套用公式1了,5的隨機數次方除以23來求余數,這個公式也是公開的,黑客知道也沒毛病,現在兩邊要各自生成一個隨機數,蒜老大生成了6,油大叔生成了15,各自生成的隨機數套入這個公開的公式,也就是蒜老大進行5的6次方要除以23得到余數8,油大叔進行5的15次方要除以23得到余數19,各自把生成的余數發送給對方。
對方收到后套用公式2,各自收到的余數的隨機數次方除以參數P求出新的余數,對于蒜老大,就是用收到的19進行6次方運算再除以23得到余數2,這里的數字6就是蒜大哥自己生成的隨機數,23就是前面定義好的參數P,對于油大叔來說,就是用收到的8進行15次方運算再除以23得到余數2,這里的數字15就是油大叔自己生成的隨機數,23也是前面定義好的參數P,現在大家可以看到兩邊得到的余數都是一樣的,都是數字2,兩邊就可以用這個數字2來對后續的對話進行加密了,沒人知道原來他們用這個2來加密后續的對話,當然了實際上的隨機數和質數其實并沒有這么簡單,通常都建議質數至少要有2048比特的長度,就是為了防止破解。
1.4、ECDH算法
ECDH是Elliptic Curve Diffie-Hellman,它一種基于ECC的密鑰協商算法。ECDH是笛福赫爾曼(Diffie-Hellman)算法的變種,它是一種密鑰協商協議,定義了密鑰怎么樣在通信雙方之間生成和交換。其思路過程與笛福赫爾曼密鑰協商算法基本相同,只是在具體的協商計算中使用ECC。
如下圖示例:Alice需要生成一個私鑰小a,然后再確定橢圓曲線上的一個點:G,這個G點是公開的,是大家都可以有的G點,接著Alice需要生成公鑰大A,公鑰就利用前面說到的橢圓曲線來運算,也就是公鑰大A等于小a點G,這里的意思就是G這個點進行點運算,次數是a,也就是G點G點G點…一共a次,得到了橢圓曲線上的點大A,現在Alice把大A和G發送給Bob,也就是大A和G是公開的,有同學可能就在想,別人知道大A和G,那小a不就很容易算出來嗎?其實前面已經說了,一定不容易,知道起點和終點,但是中間經歷多少次是非常難知道的,這就是把橢園曲線加進來的奧義。
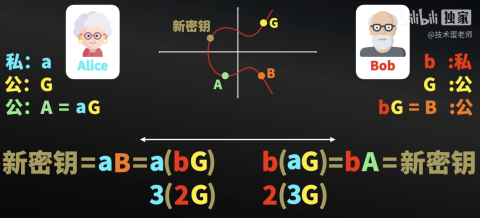
圖9:ECDH算法示例
Bob收到后,也生成了一個私鑰小b,然后生成橢園曲線上的一個新點(大B),這個大B就是G點進行小b次運算得到的,也就是G點G點G點…一共b次,現在Bob把生成的大B發送給Alice,別人知道大B和大G兩個點也很難得到小b,還是那句話:中間經歷多少次很難知道。現在Alice用私鑰小a和收到的大B進行運算得到新的密鑰,Bob用私鑰小b和收到的大A進行運算也得到了新的密鑰,這個新的密鑰就只有他們知道,也就是會話密鑰,而且這個密鑰必須是相同的。相信你對于這個運算還有點懵,你們看Alice這邊,大B其實就等于小b點G,直接從Bob那邊把等式代入就明白了,而在Bob這邊,大A其實就等于小a點G,直接從Alice那邊把等式代入就明白了,這樣一看就知道密鑰是相同的,只不過小a和小b互換了位置。如果你還看不出,假設a等于3,b等于2,不管是2乘以3,還是3乘以2,其實就等于6G了,也就是前面提及到的運算方法,這個密鑰交換過程也就是ECDHE的原理,ECDHE就是橢園曲線和DH混合起來的密鑰交換算法。
- 上一篇:DH算法圖解+數學證明 淺顯易懂
- 下一篇:沒有了
